0 引言
量子力学与信息理论是上个世纪最重要的科学发现之一。虽然这两个领域最初是分开研究的,但它们实际上是密切相关的[1]。在本文中,将传统的信息理论扩展到量子信息理论领域,并探索量子纠缠、退相干等效应所施加的限制[2],这不同于经典力学对信息存储和传输的限制[3],因为从相对熵的一个关键属性逻辑上来看[4],本文研究中的许多关键结果的推导,与“通常”表述方法需要进行区分。量子通信可以通过使用相对信息熵理论,计算量子退相干多用户信道的容量,并可以通过凸优化计算最大信道容量的范围[5]。另外,本文还讨论了量子信息熵理论的热力学[6]和量子测量的物理意义。
针对电力通信信道实时连续的情况,本文给出了基于Lebesgue积分的绝对连续的量子相对熵概率测度,并用其密度来标识。对于概率测度,可以引入相对熵和Fisher信息的定义与相互关系。在信息理论、概率和统计学中这些结论都能起到重要作用[7]。
本文在涉及相对熵函数的量子信息理论中研究各种凸优化问题[8-9],通过使用半正定规划算法求出问题的近似解[10-11]。特别地,使用这种方法来获得关于量子条件互信息与相对熵拟下限的数值[12-13]。
1 量子相对熵
此处简要介绍量子相对熵的定义及其主要性质,文献[14]给出了下述定理和性质的证明,本文不再给出详细证明。
1.1 冯诺依曼熵
定义1.1 冯诺依曼熵ρ∈Q(H )定义如下:
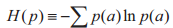
式中,p为概率函数。若ρ的谱可以基于正交基{|φa〉}a∈A分解为ρ=∑ρ(a)|φa〉 〈φa|,则冯诺依曼熵退化为香农熵p。
冯诺依曼熵有2个性质,其证明见文献[14]。
定理1.1 令ρ为互正交的密度算子,则冯诺依曼
熵 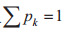 ,满足:
,满足:
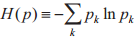 。
。
定理1.2 记混合状态向量为
|ψ〉∈HA 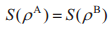
1.2 量子相对熵及其正定性
定义1.2 令ρ,σ∈Q(H),ρ到σ的量子相对信息熵定义为:
 HB上给定ρAB,有:
HB上给定ρAB,有:
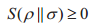
上式称为Klein不等式,等号成立的条件为当且仅当ρ=σ。
定理1.4 冯诺依曼熵的次可加性。令ρ∈Q(HA 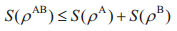
其中等号成立的条件为当且仅当ρAB=ρA 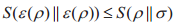
上式称为Uhlmann不等式。
推论1.1 令ρAB,σAB∈Q(HA 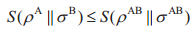
推论1.2 令ε:L(H)→L(H′)在完全正定和酉保迹映射下满足ε(I)=I,ε:L(H)→L(H′),其中I为H上的单位元,则冯诺依曼熵不递减:
 HB
HB 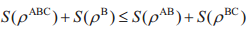
2 相对信息熵的积分表示
例如在电力系统中的信息是实时、连续的,用积分对相对信息熵进行定义,采用Lebesgue测度来定义绝对连续的实数域Rn的熵,用f(x)表其概率密度,并引入熵S(f)和Fisher信息J(f)。
定义2.1 f为Rn上的概率测度,微分熵定义为[15]:
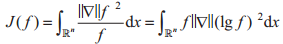
当Rn上的随机变量X有可微密度f,同样可记为J(X)=J(f)。
定义2.2 f对于g的相对熵D(f||g)定义为:
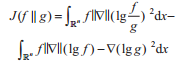
该值也是非负数值,当随机变量X和Y分别具有密度f和g时,X相对于Y的相对熵和相对Fisher信息分别定义为D(X||Y)=D(f||g)和J(X||Y)=J(f||g)。
引理2.1 令f<<g是具有有限Fisher信息J(f)<∞和J(g)<∞在Rn上的概率测度,以及有限相对熵D(f||g)<∞,然后得到:
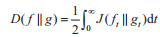
证明:对上述引理和定理简要证明如下。首先当t>0时,Fisher信息J(ft)和J(gt)有限,且随机变量X和Z的均值为0,方差为In。对于 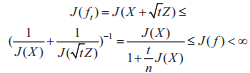
其中J(Z)=n,且方程D(ft||gt)是非递增的,则:
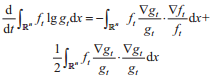
将上式带入式则得到引理结论。因为当t→∞
时, 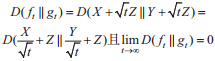
带入即可得到定理的结论。
3 量子相对熵的半正定优化
3.1 纠缠辅助信道容量
在前面两节对离散和连续情况下量子相对熵的定义和计算方法,可以进一步定义量子信道容量,并采用凸优化算法得到最大容量。考虑量子信道,具有输入A和输出B, Cea表示为纠缠辅助经典信道的能力。如果允许发射机和接收机共享任意纠缠状态,可以通过信道可靠地传输的经典比特量。记密度集合A算子D(A),量子通道的纠缠辅助经典能力具有简单的最大化表达式:
 E,即对于任意算子X,信道可表示为ψ(X)=tr[UXU*],信道互信息量可定义为:
E,即对于任意算子X,信道可表示为ψ(X)=tr[UXU*],信道互信息量可定义为:
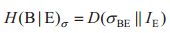
由于H(B|E)和H(B)在σ=UρU*上是凹的,因此在ρ上S(ρ||ψ)是凹的。
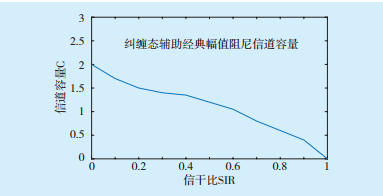 图1 纠缠辅助经典振幅阻尼信道容量Fig.1 The entanglement assisted classical amplitude damping channel capacity
图1 纠缠辅助经典振幅阻尼信道容量Fig.1 The entanglement assisted classical amplitude damping channel capacity
考虑振幅阻尼信道,信干比记为γ,计算纠缠辅助状态下振幅阻尼信道的容量,纠缠辅助经典振幅阻尼信道容量如
3.2 量子退相干信道容量
量子信道的(无辅助)量子容量Q(ψ)是能够可靠地在信道ψ传输的量子比特数量(量子位),可表示为:
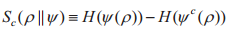
上述定义中,ψc表示信道ψ的互补信道。若ψ为环境E下由A到B的信道,其对等映射表示为ψc:L(A)→L(B)、U:A→B 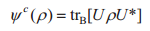
在退相干信道下,如果存在信道ε:L(B)→L(E′)且E′E,则有ψc=ε°ψ。若信道退相干,可以忽略式的极限条件,在ρ中SC是凹的。这种情况下,假设ψc=ε°ψ且令W:B→E′ 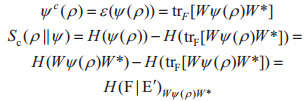
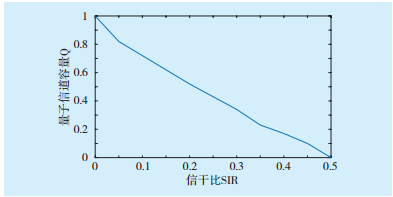 图2 振幅阻尼受限量子信道容量Fig.2 Amplitude damping confined quantum channel capacity
图2 振幅阻尼受限量子信道容量Fig.2 Amplitude damping confined quantum channel capacity
由于条件熵是凹的, 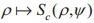 是凹的。
是凹的。
3.3 纠缠态相对熵
状态x和x可分离的凸集定义为:
 B)中的两分状态ρ,纠缠态下相对熵从ρ到S的距离定义为:
B)中的两分状态ρ,纠缠态下相对熵从ρ到S的距离定义为:
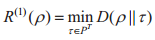
同样可以定义半正定规划的k次分割距离R(k)(ρ)。
3.4 可恢复的相对熵和条件相互信息
考虑一个三方状态ρABC在希尔伯特空间A  C上的定义,给定B的A和C的条件相互信息定义为:
C上的定义,给定B的A和C的条件相互信息定义为:
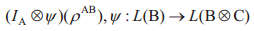
这里ψ是量子信道,对应作用于B上的三元组。
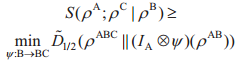 Fig.3 Comparison of the mutual entropy and the relative entropy
Fig.3 Comparison of the mutual entropy and the relative entropy 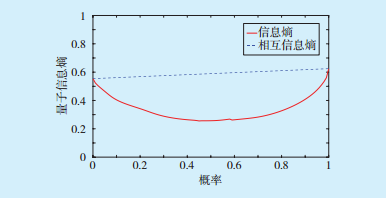 图3 互信息熵与相对熵的比较Fig.3 Comparison of the mutual entropy and the relative entropy
图3 互信息熵与相对熵的比较Fig.3 Comparison of the mutual entropy and the relative entropy
4 结语
本文论述了量子相对信息熵的定义,及其在实时连续系统中与Fisher信息量的关系,最后通过半正定规划法计算了量子纠缠辅助信道、量子退相干信道的容量,以及互信息熵与相对熵不等式的数值验证,以上结论可以用于实时或离散量子通信系统的容量计算。