图6-2给出了斯洛伐克东部电力公司全部730天的每天中每半个小时的电力负荷数据。由图6-2可以看出，电力负荷数据在年份上也表现出明显的周期性,730天的数据正好是两个周期。图6-3给出了每天的电力负荷曲线，为了比较清晰地表示该曲线，截取其中50天的负荷数据。从图6-3可以看出，电力负荷的数据呈现出明显的周期性，周期是以一个星期为单位的。另外，对于数据分析发现负荷序列还是一个以24h为周期的一个时间序列。图6-4 为截取的序列中连续6天的负荷数据。从图6-4可以看出，该序列明显的呈现周期性，并且周期为24h。综上分析可以看出，负荷序列呈现出多周期性，这样的多周期性特征可以很好地辅助多尺度的预测，但是针对按天负荷预测以及按小时的短期负荷预测，目前还没有将这种周期性考虑进负荷预测的模型出现。
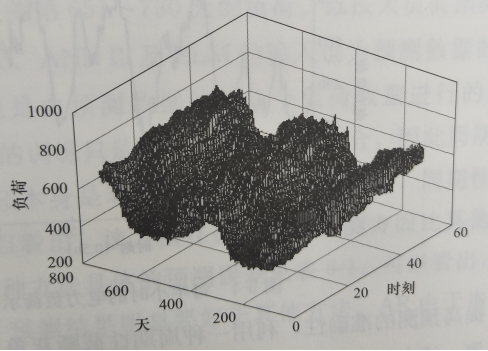
图6-2 两年的电力负荷三维图
电力负荷序列从数据特征上有明显的周期性。数据的周期性特性对于序列预测是一个重要的辅助特性。为了有效利用序列的周期性特征来提高预测的准确性，利用一种周期性截断灰色系统来对电力负荷进行预测。该方法通过周期截断累加生成操作实现序列的累加，实现序列周期性特征的表达。并且采用该方法后，时间上最近的一个周期对预测结果的影响最大，也符合实际的序列预测分析。
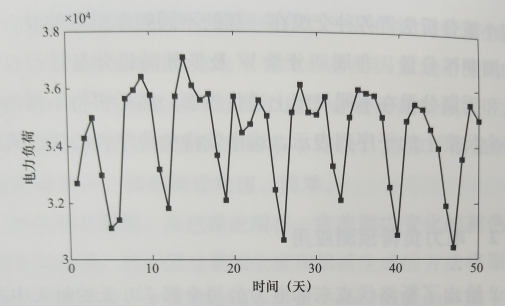
图6-3 每天的电力负荷曲线
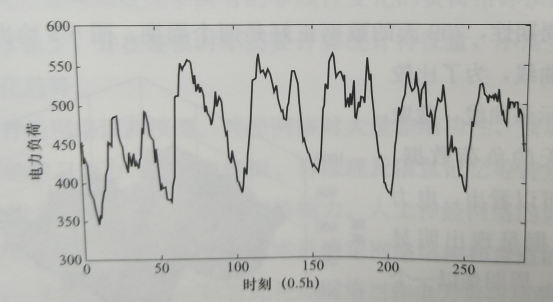
图6-4 每半小时的电力负荷示例曲线
为了将所用模型与其他方法作比较，采用归一化均方误差(NMSE)和绝对平均误差(MAPE)作为误差准则，归一化均方误差定义为：
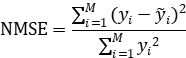
式中：yi是原数据;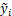 
是预测数据;M代表预测点的数量。
另一个测量法称为绝对平均误差(MAPE)。绝对平均误差被视为标准的统计性能指标之一
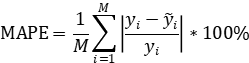
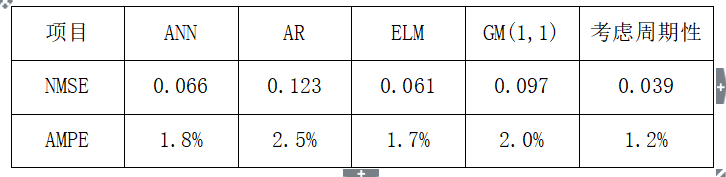
为了证明方法的有效性，将所提方法的结果与传统神经网络(ANN)，自回归模型(AR)，极限学习机模型(ELM)以及灰色系统G(1,1)模型做对比，进行了两个尺度的电力负荷预测，一个是以天为单位，一个是以半小时为单位。图6-5给出了几种不同方法的按天负荷预测结果，为了更好地展示预测结果，截取了其中2个周期进行显示。在这个测试中，预测第651--730天的负荷。以按天负荷预测时，选取的截断周期为7天。ANN以及ELM的输入也为预测数据的前7个数据，AR的拟合也是由预测数据的前7个负荷数据进行的。但是由于ANN以及ELM的训练只是整个样本集上的拟合，因此周期性很难被直接利用。而AR本身是对所有数据集的整体拟合，周期性也很难利用。从图6-5可以看出，该方法在按天负荷预测方面比其他几种方法准确度更高。几种方法具体的预测误差见表6-1。可以看出利用了周期性特征以后，预测结果明显要好于其他方法。AR由于本身线性拟合的缺陷导致预测结果最差。GM(1,1)由于没有周期性截断，导致累加数据过长，严重影响了预测精度。ANN和ELM有很好的非线性拟合能力，因此结果比AR和GM(1,1)要优。由于ELM学习的时候是全局最优的，而ANN有时容易陷入局部最优，因此ELM的预测精度比ANN略高。
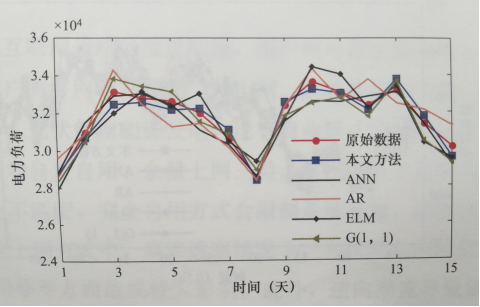
图6-5 不同方法的按天负荷预测对比
表6-1 不同方法的按天负荷预测对比结果
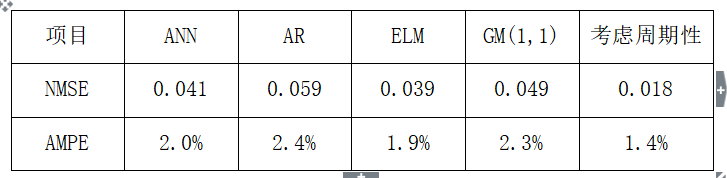
图6-6给出了几种不同方法的按半小时负荷预测结果，为了更好地展示预测结果，截取其中1个周期进行显示。在这个测试中，预测最后4天的数据。以按半小时负荷预测时，选取的截断周期为24h。ANN以及ELM的输入也为预测数据的前48个数据，AR的拟合也是由预测数据的前48个负荷数据进行的。从图6-6可以看出，考虑周期性的方法预测拟合效果要优于其他方法。表6-2给出了几种方法的具体预测结果对比。
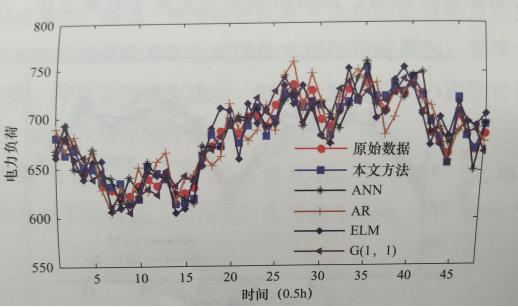
图6-6 不同方法的按半小时负荷预测对比
表6-2 不同方法的按半小时负荷预测对比结果
电力负荷的预测对电力系统调度和电力生产计划制订有着重要影响。电力负荷时间序列有着明显的周期性特征。但是目前所有的模型只是从数据本身进行建模分析，都没有很好地利用电力负荷序列的周期性特性。而数据的周期性特性对于序列预测而言是一个重要的辅助特性。为了能进一步提高负荷预测的准确性及稳定性，提出一种周期性截断灰色系统来对电力负荷进行预测。该方法改变了传统的灰色系统的累加方式，通过周期截断累加生成操作实现序列的累加，并且利用一个修正参数来提高预测的准确性和可靠性。该模型有效地利用了序列的周期性特性，提高了预测的准确性及可靠性。通过两个实际负荷序列的测试表明考虑周期性的方法比传统的神经网络、极限学习机、自回归模型以及传统的灰色系统模型准确度更高。
