系统的控制变量包括每个调度周期内的蓄电池开关状态XB(t)、 XG(t)市电开关状态和各个可控负荷的开关状态Xi(t),取1时表示设备接入系统,取0时表示断开。模型求解时,首先根据每组解的控制变量取值和负荷功率确定各个调度周期中PB(t)和PG(t)的大小,模型的供电状态判断流程如图6-8所示。
由图68可知,在默认蓄电池接入系统进行充放电的条件下,模型先判断该时段光伏功率是否大于负荷总功率,大于则进行求解充电功率,反之求解放电功率。然后将默认的蓄电池功率乘以蓄电池实际开关状态求解电网功率,再更新蓄电池实际功率。
协同调度模型是一个包含多种约束条件的0-1规划问题,采用二
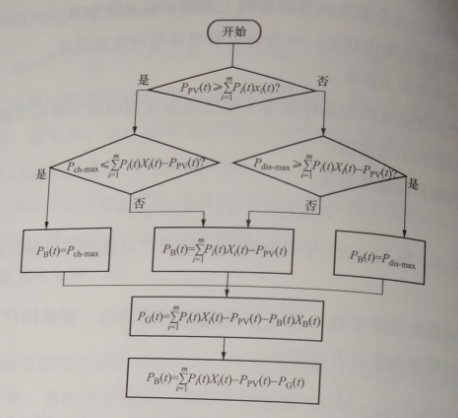
图6-8协同调度策略流程
进制粒子群(BPSO)算法对模型进行求解。首先初始化一群随机粒子,并追随当前的最优粒子在解空间中搜索,迭代找到最优解。d维搜索空间中第i个粒子的位置为Xi,=(Xi,1,Xi,2,…,Xi,d)、速度为Vi=(Vi,1,Vi,2…,Vi,d)。每次迭代中,粒子跟踪局部最优解和全局最优解,并根据式(6-13)和式(6-14)更新自己的速度
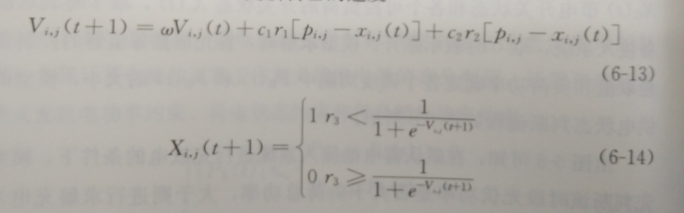
式中:w为惯性权因子;c1和c2为正学习因子;r1,r2,r3均为0~1之间均匀分布的随机数。
由于模型中全局约束条件较多,用罚函数法不易获得可行解,所以对粒子初始化和速度更新策略时进行了改进。图6-8所示的供电状态判断流程图已经处理了上式的约束。当不满足蓄电池的荷电状态约束和温控负荷约束时,则强制改变对应变量的位置,通过式(6-15)进行位置更新
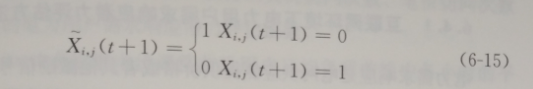
计算出粒子更新速度后,针对对应的主动性负荷控制变量,只将速度最大的变量及其后续的N个变量置1,N为设备工作持续的周期数,其他调度周期的控制变量全部置0,求解模型的流程如图6-9所示。
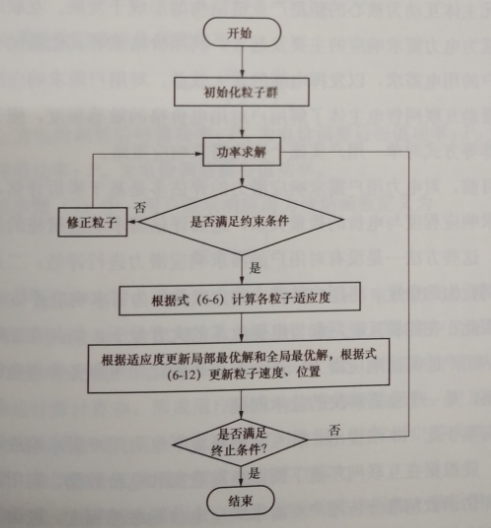
图6-9求解流程