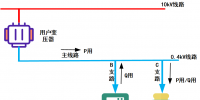
第四节 热经济学分析法
一、热经济学的产生
㶲分析法在能量有效利用和节能分析工作中发挥着很大的作用,它可以对系统能量和能质利用进行科学评价,给出技术上的最优方案,提供技术决策的科学依据。但是从工程经济学的角度来考虑,对于一个工程系统,其技术方案的最终决策,不但要求技术上优越,还必须要求经济上合理。然而,在用㶲分析法对能量系统进行分析评价时,时常会遇到的“节能不省钱”的问题。例如,从㶲的角度去分析评价一个方案可能是合理的,但是在经济上却未必一定是最佳的,甚至还可能是“费钱”的,以致出现“得不偿失”的情况。因此,仅从㶲的角度去分析问题,在经济合理性上具有局限性。另外,从实际使用与经济性的角度来考虑,不同形态能量所具有的单位㶲值并不等价。即使是同种能量形态的每单位㶲值,也并非等价。由于热力学的势参数焖是综合运用热力学第一定律和第二定律而导出的,表示能量的可无限转换部分,具有在使用中消耗的商品属性,因此㶲适合于与货币成本相联系。因此,为了考虑实际过程中㶲的不等价性和经济因素,一种可行的方法便是对“佣”赋以“价值”,即考虑不同部位和不同形态的㶲的价值是不同的,因而在㶲的基础上,把不等价性和经济因素反映在㶲的“单位”上,这就是所谓的“㶲的价值化”。于是,20世纪60年代,一种将㶲分析法与经济因素相结合的交叉学科即热经济学或称㶲经济学便应运而生了。
二、热经济学分析法概述
热经济学是基于热力学和经济学的交叉而产生的新兴学科,主要研究建立在热力学分析基础之上的经济活动。㶲经济学在热力学量度与经济学量度之间找到一个适当的平衡,借以全面而正确地反映用能系统载能价值流的运动规律,以期得到产品的单位成本最小、经济效益最佳的最优结果。热经济学分析法有两种基本思路:
(1)把要分析的系统放到两个环境中进行考察:一个是物理环境,描述该环境的参量为热力学的物理量,如温度、压力和化学势等;另一个环境是经济环境,描述这个环境的参量是一系列的经济信息,如价格、成本和利润等。物理环境是自然环境,受能量守恒等一系列自然定律的约束;经济环境虽不受这些自然定律的约束,但要遵循一切经济规律而不能违反。
(2)把系统中(包括系统与环境之间)相互作用的物质、能量、信息、设备、现金及人员都看成“流”,这些流从系统或环境的某一部分流人或流出,在流动过程中严格遵守物理环境和经济环境的有关规律,可以用一系列数学方程来描述这些规律。这些数学方程通常包括质量平衡方程、能量平衡方程、㶲平衡方程以及经济平衡方程,经济平衡方程也可称为成本平街方程。在热经济学中,成本平衡方程的建立是重点。
热经济学分析法是热力系统分析的强有力工具,特别适用于复杂工程(能量)系统的综合优化、节能分析、改造设计、系统运行性能评估与故障诊断、热力系统成本计算等技术问题。采用热经济学分析法,可以详细描述整个生产过程中产品成本的形成过程,并进行合理的成本评估,同时也便于把生产过程的燃料消耗成本和设备的投资、折旧、运行、维护、检修和管理成本相联系,按能量成本和非能量成本进行统一核算。
三、热经济学分析法的主要模式
1.“孤立化”模式
“孤立化”模式是由M.Tirbsu创立的,其基本思想是将热力系统划分为若干子系统,并使各子系统孤立化,通过对子系统逐个寻优,以局部优化代替总体进行优化,而达到全局最优的目的。孤立化模式应用的前提条件是各子系统在热经济上孤立化、互不影响,否则就会违背“系统的各个局部都为最优就意味着系统全局最优”的原则。因此,后人就将此第一次出现的热经济学命名为孤立化模式的热经济学。事实上,热力系统各子系统之间在热经济上孤立化条件很难满足,因此这种热经济学模式现在已经很少使用,除非在理论上有重大的突破,否则难以继续发展下去。
2.代数模式
代数模式是热经济学分析法中比较经典的一种模式,它主要采用会计统计的方法进行热经济学分析,因此也称为会计模式。代数模式中采用的会计法,即热经济学会计法与一般财务会计法基本相同,只是它所统计的内容不是现金,而是能量系统中的物质流、㶲流和现金流。在运用热经济学会计法时,一般要进行两个方面的统计和计算,一方面是热力学的统计和计算,如系统中的各股物流与㶲流的分布以及这些能流的焓值和㶲值;另一方面是经济学的统计和计算。在进行计算时,主要是建立能量平衡方程、物质平衡方程、㶲平衡方程、成本平衡方程来求解,以获得相应的结果。例如,在进行热力学统计和计算时,可列出系统的能量平衡方程和物质平衡方程,通过计算求取系统中各子系统的能量费用和非能量费用,以及各股㶲流的㶲单位价格。
各平衡方程的表达式可表示如下:
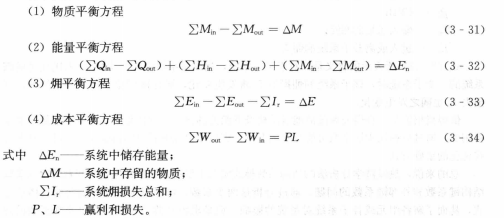
当系统稳定流动时,△M和△E均为零。以上的描述中M代表物流,W代表现金流,Q代表热量交换的数量.H代表能量流的焓值。下标out和in分别表示流出和流人各个子系统的流。
如上所述,代数模式主要运用会计统计的方法给出在系统各部位上㶲流及经济流的分布,以发现哪些地方的改进潜力最大,但它也有局限性,那就是它不能从系统整体分析的角度给出系统的某一局部改进或某一参数改变对全系统带来的影响。而一种称为“优化模式”的热经济学分析法恰好能弥补代数模式的这些不足。作为最早出现在热经济学分析法里的两种模式,代数模式和优化模式的使用在热经济学分析中并不是相互排斥的,而是相辅相成的。因此,在进行复杂方案的分析及比较时,常常把代数模式和优化模式结合起来一起使用,即先用会计统计法把大量的可行性方案进行筛选,找出其中的缺陷以及需要改进的方向,然后再进行热经济学优化,以期得到最佳方案。
3.结构系数模式
热经济分析法的结构系数模式主要是在选定的运行参数下,找出局部不可逆损失与系统整体不可逆损失、局部㶲流与系统㶲输入之间的关系。该模式能够如实描述一个系统内部各组元在热力学上甚至经济学上的内在联系,因此可用于研究一些实际过程。通常可以用结构键系数(CofficientofStructuralBonds,CSB)来描述系统局部不可逆损失与系统整体不可逆损失之间的关系,而用外部键系数(CofficientofExteriorBonds,CEB)来描述系统局部㶲流与系统㶲输入之间的关系。CSB和CEB的表达式分别表示如下

式(3-35)所表示的含义是:对于某一系统,当改变系统中某一参数Xi来优化组成该系统的一个子系统时,该子系统的㶲损失It将发生变化,同时该变化必将引起系统的总㶲损失Ik也随之发生变化。
值得指出的是,在研究系统的能量结构及其组元的热经济学优化中,结构键系数是非常有用的。通过分析结构键系数可能变化的范围,就可知道此时系统结构的变化状况,从而寻找优化的最好方式。
总的来说,热经济学分析法的结构系数模式实际上是把系统参数优化的问题转化为求解结构键系数和外部键系数的问题,通过分析这两个系数,可以得到系统各组元的具体表达式,从而了解各组元或各子系统对系统的影响。但是求解这两个系数是一个非常复杂的过程,并且对于一个复杂的热力系统,如果要确定系统中每个参数的具体表达式,有时也是不切实际的。因此在系统分析中应该根据具体情况来定。
4.矩阵模式
热经济学分析法的矩阵模式,也称为符号模式,是在㶲成本理论的基础上建立起来的,即使用符号或矩阵计算技术来建立更为通用的热经济学模型,以便分析系统中各组件的局部消耗对系统外部资源消耗的影响。热经济学分析法的矩阵模式能够解决很多传统方法无法解决的问题。例如,基于多种(物理、经济和环境等)标准的多产品成本分摊、多目标的全局和局部优化、辨识复杂能量系统内部各组件能量降的原因及其相互影响、各种可行设计方案之间的评价和优选、能源审计等。