第二节 电力企业的资金分析
一、资金的时间价值
作为电力企业的决策人员来说,在商品经济分析中应建立一个重要的概念:货币具有时间价值。所谓货币的时间价值就是货币在流通过程中所产生的新的价值。
资金的时间价值的具体表现就是利润和利息。利润是指对投资过程而言的,利息是指对借贷而言的。例如,年初从银行贷款100万元,年利率为10%,明年初应偿还110万元,后年初就应偿还121万元。如此,10万元和21万元就是100万元资金的一年和二年的时间价值。
1.利息
利息是借款人支付给贷款人的报酬。当电力企业向国家银行取得贷款时,利息则是企业支付给银行的一部分纯收入,以有列于节约使用资金,促进资金周转,加强经济核算和增加积累;而企业向银行存款时,银行对电力企业也付一定的利息,其目的在于鼓励节约,使闲置资金用于国家建设。
利息分单利和复利两种,所谓单利只按本金计算利息,累计起来的利息不再计利。例如借款100元,借期3年,每年按10%标准还利,则第3年未应付本利和为loo+loo×0-1×3-130(元)。而复利是不仅本金要逐期还息,每期累计起来的利息也要计息,如前例,第三年末按复利计算应还的本利和应为:
第一年末 100+100×0.1=110(元)
第二年末 110+110×0.1=121(元)
第三年末 121+121×0.1=133.1(元)
这比用单利法多计利息3.1元。在计算货币的时间价值时皆采用复利法。
2.利率
利率系指一定时期内利息额与贷出金额的比率,即

利率有年利率,月利率和日利率之分,是根据国家客观经济条件有计划规定的。
3.名义利率
名义利率是挂名的、非有效利率,时间是以一年为基础,每年只计息一次的利率,用r
表示。
名义利率一周期利率×每年复利周期数
例如,存款100元,计息周期为3个月,每个利息期的利率为3%,则年利率为12%。此处,12%为名义利率,而3%为周期利率,即
r=3%×4=12%
4.周期利率
它是将名义利率按同等标准分n次计息,即
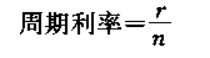
5.实际利率
实际利率是按每年计息期数复利计息所得的利率,实际利率是有效利率。这就是说,若以周期利率计算年利率,并考虑资金的时间价值,这时的年利率便是实际利率。
通常所说的年利率都是指名义利率,如不对计息时间加以说明,则表示一年计息一次,这时名义利率等于实际利率。例如,名义利率为6%,每年计息一次,实际利率也是6%。若计息期短于一年,例如可按半年、季,月、周计息,则每年计息次数为2、4、1 2、52次。计息次数越多,实际利率比名义利率越高。就前例而言
本利和=100 *(1+0* 03)2 =106. 09(元)
利息=106.09-100=6.09(元)
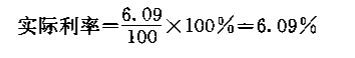
因此,实际利率力6.09%,大于名义利率6“由
由此可见:①名义利率对资金的时间价值反映得不够完全;②实际利率反映资金的时间价值;③计息周期越短,实际利率与名义利率的差值越大。
如设i为实际利率.r为名义利率,订为计息期数,P为年初投资现值,F为本利和,则
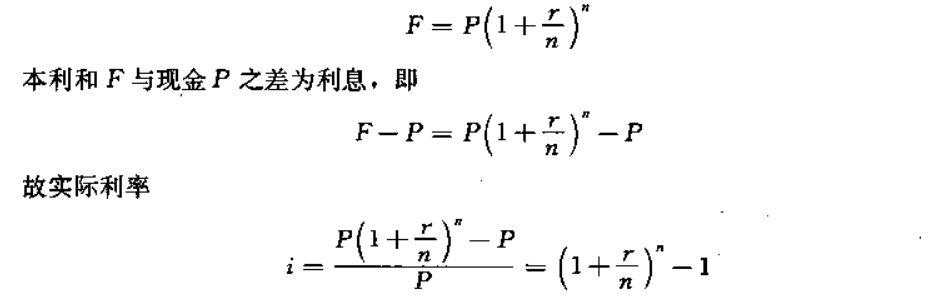
三、投资现值的折算
投资的折算有两种方法:其一是分期复利法;其二是瞬间复利法。
1.分期复利法折算投资的现值
设期初一次性投入资金的现值为P元,每期利率为i,期末所获得利息为Pi,那么,期末的本利和为

2.用分期复利法折算s为现价P的公式

上述两个例子表明:①100万元的投资.5年来的差额为61. 051万元,这就是100万元的货币在5年内所产生的时间价值;②5年后的100万元,如果年利率为10%,只与现在的62. 092万元相当。
这就是说,如将100万元的资金积压5年,则要损失掉61. 051万元。如果购买100万元的设备。5年不用,即使5年后该设备尚值100万元,也只相当现在的62. 092万元,丢掉了37. 908万元。因此,在企业经营中积压资金和购置闲置设备是极不合算的。
3.年金的分期复利公式
假定初投资的现价为P,要求在n年内等额回收,则每年的回收额则称为年金M。这里要解决的问题是:投资的现价P和年金M的换算关系。
如设年金为M,年利率为i,则第一年末回收M的现价为
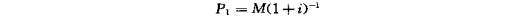


4.本利和与年金换算的分期复利公式

四、利息的计算
1.间断复利息的计算

2.连续复利息计算公式