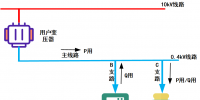
摘 要:有限的资源和随机的需求是排队论存在的基础,而在如今的社会,这种现象越发广泛和复杂。我们将要求服务的顾客和提供服务的机构组合成一个系统,称之为排队系统。这种系统存在于各个方面,本文研究的是排队论运用在通信网络中的各端业务问题。排队论系统分为优先制排队系统和非优先制排队系统,本文描述了带有非强占权优先制的排队系统,其模型为两队中其中一对带有优先制度的M/M/1的模型。根据此模型可以定义变量,画出状态转移图并列出状态方程,最后求出稳态解。通过性能分析发现,带有优先权的M/M/1模型系统与一般模型相比性能将会有所提高,这也是优先制度的体现。
关键词:排队论 状态转移 M/M/1模型
1 规定系统模型
在实际问题中,选择适当的模型,有利于更好的解决问题。这里我们采用的是带优先制度的M/M/1模型。当有n个业务公用一条线路时,事先规定好各自的优先级。本文采用的优先制度为:队伍中有n个业务公用一条线路,优先级高的一对享有优先权,只要线路有空闲时即可占用,而优先级别低的必须在优先级高的队伍无呼叫等待且线路空闲时才能占用线路,但不会强行中断正在占用线路的用户。这就是非强占权优先制排队系统。
2 定义状态变量
定义系统的变量是求解问题难易的关键,所选择的变量要便于计算,其结果要有可用性。选择的变量越多,维数越大,计算就越难复杂。通信网中业务分析常用的变量是队长和占用线数等,并且通信网中业务分析趋于稳态,很少涉及暂态,所以我们一般只求稳态解。
规定A队列和B队列,其中A队有优先权,B队只能在A队无等待着的呼叫时占用线路,占用后不会因为A队有呼叫而被强拆。
系统状态主要有两个因素:线路的繁忙,A.B两队等待处理的呼叫数。令t为线路状态,t =1表示线路占用,t=0表示线路空闲。r与s分别表示A.B两队中等待的呼叫数。r与s不包括正在传输的呼叫,因为后者可能是A队的,也可能是B队的。其中,两队的到达率分别为 和
和  ,服务率为
,服务率为  。
。
3 列出状态方程
对于M/M系统,可先画出状态转移图,直接用柯式方程列出状态方程。从一个系统的状态转移图可以清楚的看出某个状态到另一个状态的转移概率,这种方法简单明了,便于分析问题并列出状态方程。
当系统空闲时,即t =0,r与s也为0,称之为“0”状态。当t =1时,用二维矢量(r,s)代表系统状态。两队的截止队长(不包括正在传输的呼叫)分别为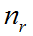 和
和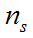 。状态转移图如图1所示。
。状态转移图如图1所示。
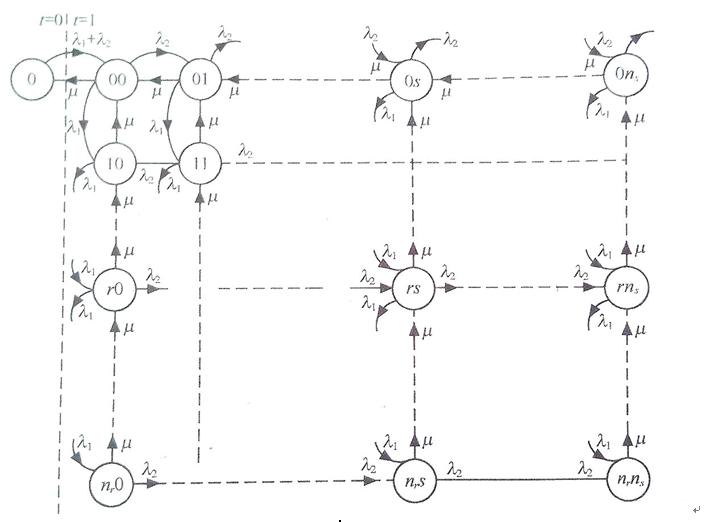
图1 非强占权优先制系统的状态转移图
图1中所体现出来的优先制度为:当r>0时,(r,s+1)状态不能转移到(r,s)状态,因为一旦有线路空闲,A队就会占用线路,就转移到(r-1,s+1)状态。由图1可写出稳态下的系统状态方程:
r =s =t =0: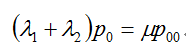
t =1, r =0, s<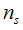 :
: 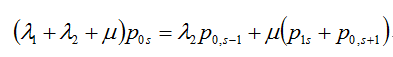
t =1, s =0, r<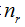 :
: 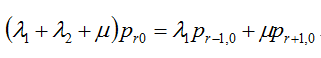
t =1,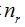 > r> 0,
> r> 0,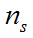 > s> 0
> s> 0 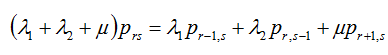
t =1, r =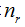 , s<
, s<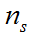 :
: 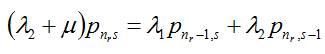
t =1, s =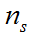 , r<
, r<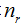 :
: 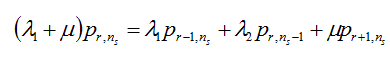
t =1, s =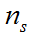 , r =
, r =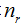 :
: 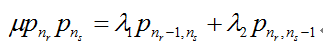
归一条件:
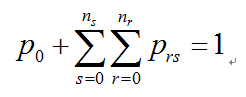
在上述方程中,如果r和s出现负数,理解为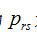 为0。上述所有公式即为系统的状态方程,这些方程构成一个二维的差分方程,求解很麻烦。
为0。上述所有公式即为系统的状态方程,这些方程构成一个二维的差分方程,求解很麻烦。
4 求解稳态状态方程
设A队为不拒绝型的,即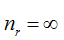 ;B队是及时拒绝型的,即
;B队是及时拒绝型的,即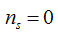 ,亦即s为0。状态方程可简化为:
,亦即s为0。状态方程可简化为:
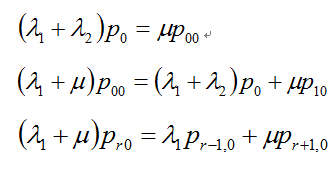
最后求解出:
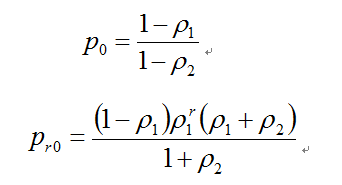
5 性能分析
由求解出的 可以得到B队的拒绝概率:
可以得到B队的拒绝概率:
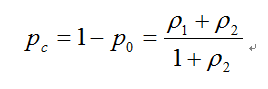
信道利用率:
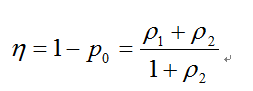
上述中
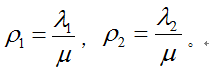
其中A队的平均等待时间为:
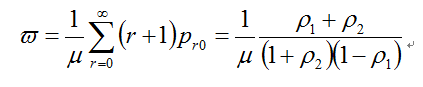
现在来分析标准M/M/1系统的性能。对于标准的M/M/1系统,即B队是不存在的,平均时间为:
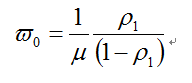
信道利用率:
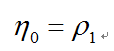
可以明显看出,利用优先制度,再加上B队列,A队的平均等待时间将会增长,信道利用率也会提高。这就表明,信道利用率的提高将会带来的后果是优先队列的等待时间增长。
参考文献:
[1]周炯槃.通信网理论基础(修订版)[M].北京:人民邮电出版社,2009.
[2]

关键词:排队论 状态转移 M/M/1模型
1 规定系统模型
在实际问题中,选择适当的模型,有利于更好的解决问题。这里我们采用的是带优先制度的M/M/1模型。当有n个业务公用一条线路时,事先规定好各自的优先级。本文采用的优先制度为:队伍中有n个业务公用一条线路,优先级高的一对享有优先权,只要线路有空闲时即可占用,而优先级别低的必须在优先级高的队伍无呼叫等待且线路空闲时才能占用线路,但不会强行中断正在占用线路的用户。这就是非强占权优先制排队系统。
2 定义状态变量
定义系统的变量是求解问题难易的关键,所选择的变量要便于计算,其结果要有可用性。选择的变量越多,维数越大,计算就越难复杂。通信网中业务分析常用的变量是队长和占用线数等,并且通信网中业务分析趋于稳态,很少涉及暂态,所以我们一般只求稳态解。
规定A队列和B队列,其中A队有优先权,B队只能在A队无等待着的呼叫时占用线路,占用后不会因为A队有呼叫而被强拆。
系统状态主要有两个因素:线路的繁忙,A.B两队等待处理的呼叫数。令t为线路状态,t =1表示线路占用,t=0表示线路空闲。r与s分别表示A.B两队中等待的呼叫数。r与s不包括正在传输的呼叫,因为后者可能是A队的,也可能是B队的。其中,两队的到达率分别为
3 列出状态方程
对于M/M系统,可先画出状态转移图,直接用柯式方程列出状态方程。从一个系统的状态转移图可以清楚的看出某个状态到另一个状态的转移概率,这种方法简单明了,便于分析问题并列出状态方程。
当系统空闲时,即t =0,r与s也为0,称之为“0”状态。当t =1时,用二维矢量(r,s)代表系统状态。两队的截止队长(不包括正在传输的呼叫)分别为
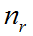 和
和
图1 非强占权优先制系统的状态转移图
图1中所体现出来的优先制度为:当r>0时,(r,s+1)状态不能转移到(r,s)状态,因为一旦有线路空闲,A队就会占用线路,就转移到(r-1,s+1)状态。由图1可写出稳态下的系统状态方程:
r =s =t =0:
t =1, r =0, s<
t =1, s =0, r<
t =1,
t =1, r =
t =1, s =
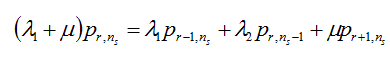
t =1, s =
归一条件:
在上述方程中,如果r和s出现负数,理解为
4 求解稳态状态方程
设A队为不拒绝型的,即
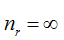 ;B队是及时拒绝型的,即
;B队是及时拒绝型的,即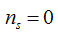 ,亦即s为0。状态方程可简化为:
,亦即s为0。状态方程可简化为:最后求解出:
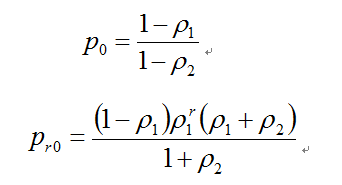
5 性能分析
由求解出的
信道利用率:
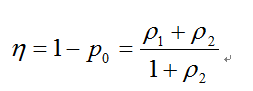
上述中
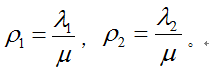
其中A队的平均等待时间为:
现在来分析标准M/M/1系统的性能。对于标准的M/M/1系统,即B队是不存在的,平均时间为:
信道利用率:
可以明显看出,利用优先制度,再加上B队列,A队的平均等待时间将会增长,信道利用率也会提高。这就表明,信道利用率的提高将会带来的后果是优先队列的等待时间增长。
参考文献:
[1]周炯槃.通信网理论基础(修订版)[M].北京:人民邮电出版社,2009.
[2]